An Introduction to Nanotechnology

Nanotechnology is defined as the study and use of structures between 1 nanometer and 100 nanometers in size. To give you an idea of how small that is, it would take eight hundred 100 nanometer particles side by side to match the width of a human hair.

While this is the most common definition of nanotechnology researchers with various focuses have slightly different definitions. For a summary of these different definitions see Definitions of Nanotechnology,

Introduction to Nanotechnology: Looking At Nanoparticles

Scientists have been studying and working with nanoparticles for centuries, but the effectiveness of their work has been hampered by their inability to see the structure of nanoparticles. In recent decades the development of microscopes capable of displaying particles as small as atoms has allowed scientists to see what they are working with.

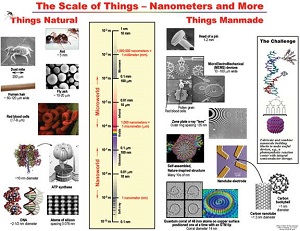
The following illustration titled “The Scale of Things”, created by the U. S. Department of Energy, provides a comparison of various objects to help you begin to envision exactly how small a nanometer is. The chart starts with objects that can be seen by the unaided eye, such as an ant, at the top of the chart, and progresses to objects about a nanometer or less in size, such as the ATP molecule used in humans to store energy from food.

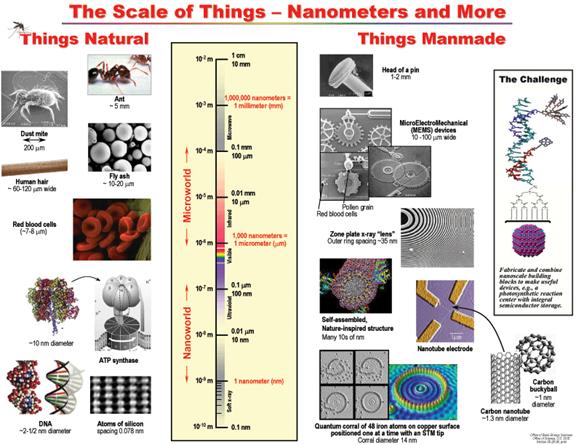
Now that you have an idea of how small a scale nanotechnologists work with, consider the challenge they face. Think about how difficult it is for many of us to insert thread through the eye of a needle. Such an image helps you imagine the problem scientists have working with nanoparticles that can be as much as one millionth the size of the thread. Only through the use of powerful microscopes can they hope to ‘see’ and manipulate these nano-sized particles. Browsing through our Nanoparticles page will help you understand nanoparticles.

Introduction to Nanotechnology Applications

The ability to see nano-sized materials has opened up a world of possibilities in a variety of industries and scientific endeavors. Because nanotechnology is essentially a set of techniques that allow manipulation of properties at a very small scale, it can have many applications, such as the ones listed below.

Drug delivery. Today, most harmful side effects of treatments such as chemotherapy are a result of drug delivery methods that don't pinpoint their intended target cells accurately. Researchers at Harvard and MIT have been able to attach special RNA strands, measuring about 10 nm in diameter, to nanoparticles and fill the nanoparticles with a chemotherapy drug. These RNA strands are attracted to cancer cells. When the nanoparticle encounters a cancer cell it adheres to it and releases the drug into the cancer cell. This directed method of drug delivery has great potential for treating cancer patients while producing less side harmful affects than those produced by conventional chemotherapy.

Fabrics. The properties of familiar materials are being changed by manufacturers who are adding nano-sized components to conventional materials to improve performance. For example piezoelectric fibers are being devloped that could allow clothing to generate electricity through normal motions.

Reactivity of Materials. The properties of many conventional materials change when formed as nano-sized particles (nanoparticles). This is generally because nanoparticles have a greater surface area per weight than larger particles; they are therefore more reactive to some other molecules. For example studies have show that nanoparticles of iron can be effective in the cleanup of chemicals in groundwater because they react more efficiently to those chemicals than larger iron particles.

Strength of Materials. Nano-sized particles of carbon, (for example nanotubes and bucky balls) are extremely strong. Nanotubes and bucky balls are composed of only carbon and their strength comes from special characteristics of the bonds between carbon atoms.  One proposed application that illustrates the strength of nanosized particles of carbon is the manufacture of t-shirt weight bullet proof vests made out of carbon nanotubes.

Micro/Nano ElectroMechanical Systems. The ability to create gears, mirrors, sensor elements, as well as electronic circuitry in silicon surfaces allows the manufacture of miniature sensors such as those used to activate the airbags in your car. This technique is called MEMS (Micro-ElectroMechanical Systems). The MEMS technique results in close integration of the mechanical mechanism with the necessary electronic circuit on a single silicon chip, similar to the method used to produce computer chips. Using MEMS to produce a device reduces both the cost and size of the product, compared to similar devices made with conventional methods. MEMS is a stepping stone to NEMS or Nano-ElectroMechanical Systems. NEMS products are being made by a few companies, and will take over as the standard once manufacturers make the investment in the equipment needed to produce nano-sized features.

Molecular Manufacturing. If you're a Star Trek fan, you remember the replicator, a device that could produce anything from a space age guitar to a cup of Earl Grey tea. Your favorite character just programmed the replicator, and whatever he or she wanted appeared. Researchers are working on developing a method called molecular manufacturing that may someday make the Star Trek replicator a reality. The gadget these folks envision is called a molecular fabricator; this device would use tiny manipulators to position atoms and molecules to build an object as complex as a desktop computer. Researchers believe that raw materials can be used to reproduce almost any inanimate object using this method.

The Nanotechnology Debate

There are many different points of view about the nanotechnology. These differences start with the definition of nanotechnology. Some define it as any activity that involves manipulating materials between one nanometer and 100 nanometers. However the original definition of nanotechnology involved building machines at the molecular scale and involves the manipulation of materials on an atomic (about two-tenths of a nanometer) scale.

The debate continues with varying opinions about exactly what nanotechnology can achieve. Some researchers believe nanotechnology can be used to significantly extend the human lifespan or produce replicator-like devices that can create almost anything from simple raw materials. Others see nanotechnology only as a tool to help us do what we do now, but faster or better.

The third major area of debate concerns the timeframe of nanotechnology-related advances. Will nanotechnology have a significant impact on our day-to-day lives in a decade or two, or will many of these promised advances take considerably longer to become realities?

Finally, all the opinions about what nanotechnology can help us achieve echo with ethical challenges. If nanotechnology helps us to increase our lifespans or produce manufactured goods from inexpensive raw materials, what is the moral imperative about making such technology available to all? Is there sufficient understanding or regulation of nanotech based materials to minimize possible harm to us or our environment? 

Only time will tell how nanotechnology will affect our lives, but browsing through the topics on the navigation bar above  will help you understand the possibilities and anticipate the future.